Skip Navigation
Skip to contents

Clin Endosc : Clinical Endoscopy

Search
Advanced Search
OPEN ACCESS
mobile search button mobile menu button

Articles

Page Path
HOME > Clin Endosc > Volume 45(3); 2012 > Article
Original Article Feasibility of Obtaining Quantitative 3-Dimensional Information Using Conventional Endoscope: A Pilot Study
Jong Jin Hyun1, Hoon Jai Chun1, Bora Keum1, Yeon Seok Seo1, Yong Sik Kim1, Yoon Tae Jeen1, Hong Sik Lee1, Soon Ho Um1, Chang Duck Kim1, Ho Sang Ryu1, Jong-Wook Lim2, Dong-Gi Woo2, Young-Joong Kim2, Myo-Taeg Lim2
Clinical Endoscopy 2012;45(3):182-188.
DOI: https://doi.org/10.5946/ce.2012.45.3.182
Published online: August 22, 2012

1Division of Gastroenterology and Hepatology, Department of Internal Medicine, Korea University College of Medicine, Seoul, Korea.

2Department of Electrical Engineering, Korea University College of Engineering, Seoul, Korea.

Correspondence: Hoon Jai Chun. Division of Gastroenterology and Hepatology, Department of Internal Medicine, Korea University Anam Hospital, Korea University College of Medicine, 73 Inchon-ro, Seongbuk-gu, Seoul 136-705, Korea. Tel: +82-2-920-5699, Fax: +82-2-953-1943, drchunhj@chol.com
• Received: July 28, 2011   • Revised: March 6, 2012   • Accepted: March 6, 2012

Copyright © 2012 Korean Society of Gastrointestinal Endoscopy

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

  • 6,659 Views
  • 72 Download
  • 6 Crossref
  • 7 Scopus
prev next
Full Article

Download PDF Download PDF

  • Background/Aims
    Three-dimensional (3D) imaging is gaining popularity and has been partly adopted in laparoscopic surgery or robotic surgery but has not been applied to gastrointestinal endoscopy. As a first step, we conducted an experiment to evaluate whether images obtained by conventional gastrointestinal endoscopy could be used to acquire quantitative 3D information.
  • Methods
    Two endoscopes (GIF-H260) were used in a Borrmann type I tumor model made of clay. The endoscopes were calibrated by correcting the barrel distortion and perspective distortion. Obtained images were converted to gray-level image, and the characteristics of the images were obtained by edge detection. Finally, data on 3D parameters were measured by using epipolar geometry, two view geometry, and pinhole camera model.
  • Results
    The focal length (f) of endoscope at 30 mm was 258.49 pixels. Two endoscopes were fixed at predetermined distance, 12 mm (d12). After matching and calculating disparity (v2-v1), which was 106 pixels, the calculated length between the camera and object (L) was 29.26 mm. The height of the object projected onto the image (h) was then applied to the pinhole camera model, and the result of H (height and width) was 38.21 mm and 41.72 mm, respectively. Measurements were conducted from 2 different locations. The measurement errors ranged from 2.98% to 7.00% with the current Borrmann type I tumor model.
  • Conclusions
    It was feasible to obtain parameters necessary for 3D analysis and to apply the data to epipolar geometry with conventional gastrointestinal endoscope to calculate the size of an object.
  • Keywords: 3-dimensional imaging; Endoscopes; Distortion; Epipolar geometry
It is difficult to get a grasp of depth with one eye. Human eyes perceive objects using two lenses separated at a fixed distance and by accommodating the eyeballs, enabling one to get 3-dimensional (3D) images. There have been many attempts to introduce 3D photography in the past and earlier attempts were done by first taking two separate images at a slightly different angle and placing the two frames on dedicated mount to get stereographic images for the viewer. However, complicated set-up and reliance on 3D glasses meant that they were too complex or cumbersome for widespread use.
Recently, 3D image began to gain attention again. Horseman/Rollei unveiled 3D stereo film camera in 2006, but there was limitation of still having to use a stereoscopic viewer to view 3D images. In 2009, Fujifilm Holdings Corporation (Tokyo, Japan) has launched the first digital 3D camera with more advanced technology enabling application of 3D sheet to the liquid crystal display monitor obviating the need of using stereoscopic viewer, thus allowing the viewers to view the 3D image directly on the screen. In addition, filmmakers are competitively producing 3D movies and enticing the public to the world of 3D technology. These recent changes seem to herald the commencement of a new era of 3D technology. The 3D imaging technique is expanding its realm, especially into the field of medicine; in fact, it has already been used in the fields such as general surgery, neurosurgery, or urology, guided by laparoscopes and robots.1,2
Since its introduction, laparoscopic surgery has revolutionized the field of surgery in many aspects such as reduced postoperative pain, shorter recovery time and hospital stay, earlier return to everyday living, fewer postoperative complications, etc. However, indirect viewing on a 2-dimensional (2D) screen rendered accurate manipulation of the instruments difficult.3 Due to poor depth perception, relative position of the anatomic structures had to be perceived mainly by touching the anatomic parts and previous experiences of the surgeon. Thus, it has been shown that compared with surgery under direct normal vision, 2D endoscopic vision impaired surgical performance by 35% to 100%.3,4 In order to overcome this problem, stereoscopic imaging was applied to laparoscopy. Although the usefulness of the stereo viewing varied among studies,5 it was proved to be beneficial for novice surgeons and in carrying out complex tasks.6
In the field of gastroenterology, 3D imaging technique has gained some attention in part for virtual colonoscopy. However, as the name implies, it is "virtual" and thus there exists discrepancies between direct and virtual visualization; virtual colonoscopy cannot accurately visualize polyps of less than 1 cm in size, cannot tell subtle differences in lesions by texture and color, and may misinterpret retained feces as polyps.7 To diagnose and discern such lesions accurately, applying and obtaining 3D images of the gastrointestinal tract with endoscopes seems to be an intriguing and a plausible idea. For the moment, diagnosis and treatment of mucosal lesion would seem sufficient with current gastrointestinal endoscopes. Nevertheless, with the advent of natural orifice transluminal endoscopic surgery (NOTES), endoscopists are now confronted with the same limitations as laparoscopic surgeons had to face, i.e., depth perception. It is very likely that conventional endoscopes will continue to be used for NOTES procedures performed via transesophageal, transgastric, or transcolonoic route. Therefore, as a first step in assessing the feasibility of applying this attractive 3D concept to conventional gastrointestinal endoscopy, we conducted an experiment to evaluate whether images obtained with conventional gastrointestinal endoscopes could be used to acquire quantitative 3D information.
Materials
To obtain data for 3D image analysis, two endoscopes (GIF-H260, Olympus, Tokyo, Japan) were placed side-to-side, fixed at a predetermined distance (12 mm) from each other, and endoscopic stereo-images of an object were obtained. The object observed with endoscopes was a Borrmann type I tumor model made of clay that was 40 mm high and 43 mm in diameter.
Image preprocessing
In the endoscopes, fish-eye lens are utilized to get a wider field of view of the gastrointestinal lumen. However, the use of fish-eye lens causes barrel distortion producing images quite different from the true image as shown in Fig. 1. The image becomes more distorted as the object is observed at a closer distance. In addition, when a 3D image is projected on a 2D plane, another distortion called perspective distortion occurs and the resulting image without correction of the distortions would not be fit for further analysis and be prone to a wide range of errors. Therefore, before processing the acquired image for further analysis, the endoscopes were calibrated by correcting the barrel distortion and perspective distortion (Fig. 2). Endoscope calibration was carried out by using MATLAB Toolbox (MathWorks, Natick, MA, USA) which enabled us to acquire the focal length (f) of the fish-eye lens in the endoscope. Afterwards, the obtained image was converted to gray-level image and the characteristics of the image was obtained by edge detection. Finally, data on 3D parameters were measured by using epipolar geometry, two view geometry, and a pinhole camera model.
Epipolar geometry, two view geometry, and a pinhole camera model
There are few terminologies that are worth mentioning. Stereo-image is an image captured by two cameras. Matching is the process of finding the corresponding position of the point on the left image with that of the right image. Disparity indicates relative position of a point in an image (Fig. 3).
After stereo-images have been taken from different viewpoints and the images have been preprocessed, epipolar geometry then describes the relation between the two resulting views. In brief, epipolar geometry is a simple but essential geometric concept which explains that when multitude of points connecting M, M1, M2, etc. are observed from CL, it is observed as a dot on its image plane as mL, but when these points are observed from CR, it is observed as a line on its image plane as eR-mE (Fig. 4). It is then assumed that the cameras are pinhole cameras (CL and CR), which has image planes in front of the focal point-unlike real cameras which have image planes behind the focal point-and that all dots lie on the same plane called epipolar plane which connects M, CL, and CR. This is the fundamental concept in reprocessing and calculating the parameters of 3D images.
Now, we take the epipolar plane to calculate the distance between the camera and the object by triangulation using two view geometry (Fig. 5). In this figure we can see that the image plane has been placed behind the focal points as is with real cameras. The f has been previously obtained by calibrating the camera, which in our case is the endoscope. The distance between the two endoscopes (d12) has been predetermined. When the object "M" is seen from two endoscopes CL and CR, two corresponding images mL and mR can be obtained on the each image plane of CL and CR. Since mL and mR are images of the same object, it can be matched, but due to the difference in the relative location of the object that is projected onto corresponding planes, there is disparity (v2-v1). Equation on disparity is as follows:
(Equation 1)
ce-45-182-e001.jpg
If we substitute all the known and obtained variables, we can calculate the distance between the cameras and the object (L).
After "L" has been determined, we can calculate the height of the object (H). This can be done by using a pinhole camera model in which f is focal length, h is the height of the projected image, and L is the distance obtained from the previous equation (Fig. 6). When we substitute these data into the equation below,
(Equation 2)
f : h=L : H
we can get the calculated height of the actual object.
Stereo-images were obtained at three different distances from the Borrmann type I tumor model: 30, 40, and 50 mm. The f obtained by calibrating the endoscope using MATLAB Toolbox at 30 mm from the Borrmann type I tumor model was 258.49 pixels. Two endoscopes were fixed at a predetermined distance, 12 mm (d12). The corresponding points of the Borrmann type I tumor model obtained by each endoscopes (374, 241) and (265, 231), were matched, and the disparity v2-v1 was calculated as 106 pixels (Fig. 7). When all these values were substituted into the equation 1, the length between the camera and the object (L) was 29.26 mm (Table 1). The height and width of the object projected onto the image (h) was then substituted into the proportional equation 2, and the result was 38.21 mm and 41.72 mm, respectively (Table 2). The values obtained at 40 mm and 50 mm are also shown in Tables 1, 2.
The measurement error of the distance between the endoscope and the current Borrmann type I tumor model ranged from 0.18% to 2.46%, and that of the height and width rang-ed from 2.98% to 7.00%.
Through this experiment, we could see that acquiring quantitative 3D information by applying epipolar geometry, two view geometry, and a pinhole camera model to calculate the size of an object was feasible with conventional endoscopes. The pinhole camera model accompanied by correction of barrel and perspective distortions, as had been done in our study, is known to be a fair approximation for most of the narrow-angle and wide-angle lenses.8,9 However, since there is an inherent distortion of a fish-eye lens that makes it difficult to be considered a mere deviation from a pinhole camera model,10 errors have occurred in our measurements. Therefore, empl-oying a generic camera model proposed by Kannala and Brandt,11 which is based on viewing a planar calibration pattern instead of perspective projection used by the pinhole camera model, could have conferred greater precision in obtaining parameters. For simplicity of calculation, however, we have applied the pinhole camera model in our study to calculate the H and have produced a fair approximation. Nevertheless, applying the generic camera model should be considered in reconstructing 3D images in the future studies.12 In addition, the errors in measurement might have been due to the fact that the feature points of an object could not be accurately extracted. This seems to have risen because the tumor model we made did not have definite edges. If the model used for measurement had been a cube or an object with definite edges, fe-ature point extracting and matching would have been facilitated. However, we intended to simulate an actual tumor even though this had been a source of errors. One way to overcome feature point extracting and matching problems with an actual tumor could be by applying the method called circular hough transform. In a preliminary study by our group, the circular hough transform was shown to be able to extract feature points from 2D tumor stereo-images to recover information with good accuracy.
Light source seems to be another problem in obtaining images. In the initial phase of this experiment, we tried to obtain images by using two different models of endoscopes, GIF-H260 (Olympus) which had stronger illuminating power and GIF-Q260 (Olympus) which had relatively weaker one. However, while the image taken with GIF-H260 took on a true color, the image taken with GIF-Q260 took on a bluish hue, being dominated by the stronger light. The differences in illuminating power of the two endoscopes lead to skewed color images. In addition, the size of the projected image was different with each endoscope. Since it should be like capturing images individually and twice, once with the right eye and another with left eye, perfect synchronization of the right and left images is mandatory and is of the utmost importance. When different types of endoscopes were used, this could not be achieved due to the lack of concordance of range and angle of the view. Therefore, we decided to use two endoscopes of the same model and had equal illuminating power. Nevertheless, we were faced with other problems: light interference and mixture or addition of lights. Although two endoscopes of the same model were used, they were exact twins but two separate endoscopes with discordance of brightness, color, and image quality. The pictures taken during our preliminary experiment demonstrate artifacts resembling a comet's tails, as if the tumor model in the picture was moving towards each other and leaving behind its trace (Fig. 8). This is due to light interference or discordance of brightness. In addition, the use of two light sources of equal illuminating power resulted in the mixture or addition of lights rendering only a white tone. This is due to discordance of color. This could be overcome by making an endoscope with two lenses that uses a single light source which in current endoscopes would be two illumination lights that are synchronized. Recently, even more ideal and unique 3D system has been developed by Wasol (Seoul, Korea). Unlike all the other 3D systems that are based on two camera system, Wasol's 3D endoscope applies only one camera. Changing the path of light using the difference in density between objects enables one to obtain stereo images.13 This novel 3D system would essentially eliminate the discordance problems related to zooming, focusing, and aligning when two lenses are used.
In addition to the problem with light source, another pro-blem to overcome was that the 3D parameters acquired from our study were calculations from 2D still images and were not real time based. Although we have demonstrated the possibility of extracting 3D information from 2D images using conventional endoscopes, applying the endoscope system presented by Nakatani et al.14 which has four laser beam sources attached to the endoscope could also be considered in constructing future 3D endoscopes to facilitate the acquisition of real time measurements of the size and position of an object.
In our study, two separate endoscopes were used alternately to recover a set of image. Hasegawa and Sato15 devised a 3D endoscope to realize high-speed 3D measurement which also incorporated laser scanning. This endoscope was a rigid endoscope that has two lenses in the shaft allowing binocular 3D viewing and was subject to some measurement errors depending on the movement of the object being observed. Although it might be necessary at first to use a binocular viewer or other special viewer to observe a lesion in 3D, rapidly advancing technology will enable adopting a 3D display that will allow endoscopists to view the lesion right on the screen. In addition, the problem of increased endoscope diameter due to the incorporation of two lenses might be overcome by adopting the above mentioned Wasol's 3D system.
We still have a long way to go before 3D technology is fully integrated into endoscopy. However, with further advances in technology, it will lessen the burden of surgeons during operation and help the gastrointestinal endoscopists during such procedures as endoscopic submucosal dissection and NOTES procedures. They will not only be able to observe a lesion in real time 3D view but measure depth, exact size, volume, etc. to aid their judgment during observation and procedure. Subtle mucosal change might also be discerned with greater accuracy. Further progress will enable us to characterize the lesions leading to formulation of a new classification of polyps and cancers, new evaluation index of response to chemotherapy, and novel criteria for assessing ulcer healing response by measuring the 3D structure of an ulcer.16 There is no doubt that problems related to depth perception during NOTES procedures, as has occurred with conventional laparoscopy, could be overcome. Applying 3D technology to endoscopes will add new dimension to endoscopy. Furthermore, easy to use 3D endoscopes will prove to be as important a step in imaging as the introduction of digital endoscope a decade ago. Although there are many improvements to be made before meeting our expectations, the doors for future development of 3D endoscopy are open to revolutionize and make great contribution in the progress of a new era of endoscopy. All endoscopists should keep their eyes open since 3D endoscopy might prove to be something more than meets the eye.
  • 1. Fox WC, Wawrzyniak S, Chandler WF. Intraoperative acquisition of three-dimensional imaging for frameless stereotactic guidance during transsphenoidal pituitary surgery using the Arcadis Orbic System. J Neurosurg 2008;108:746–750.ArticlePubMed
  • 2. Tan GY, Goel RK, Kaouk JH, Tewari AK. Technological advances in robotic-assisted laparoscopic surgery. Urol Clin North Am 2009;36:237–249.ArticlePubMed
  • 3. Taffinder N, Smith SG, Huber J, Russell RC, Darzi A. The effect of a second-generation 3D endoscope on the laparoscopic precision of novices and experienced surgeons. Surg Endosc 1999;13:1087–1092.ArticlePubMed
  • 4. Perkins N, Starkes JL, Lee TD, Hutchison C. Learning to use minimal access surgical instruments and 2-dimensional remote visual feedback: how difficult is the task for novices? Adv Health Sci Educ Theory Pract 2002;7:117–131.ArticlePubMed
  • 5. Hofmeister J, Frank TG, Cuschieri A, Wade NJ. Perceptual aspects of two-dimensional and stereoscopic display techniques in endoscopic surgery: review and current problems. Semin Laparosc Surg 2001;8:12–24.ArticlePubMed
  • 6. Pietrabissa A, Scarcello E, Carobbi A, Mosca F. Three-dimensional versus two-dimensional video system for the trained endoscopic surgeon and the beginner. Endosc Surg Allied Technol 1994;2:315–317.PubMed
  • 7. Wood BJ, Razavi P. Virtual endoscopy: a promising new technology. Am Fam Physician 2002;66:107–112.PubMed
  • 8. Swaminathan R, Nayar SK. Nonmetric calibration of wide-angle lenses and polycameras. IEEE Trans Pattern Anal Mach Intell 2000;22:1172–1178.Article
  • 9. Heikkila J. Geometric camera calibration using circular control points. IEEE Trans Pattern Anal Mach Intell 2000;22:1066–1077.Article
  • 10. Miyamoto K. Fish eye lens. J Opt Soc Am 1964;54:1060–1061.Article
  • 11. Kannala J, Brandt SS. A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses. IEEE Trans Pattern Anal Mach Intell 2006;28:1335–1340.ArticlePubMed
  • 12. Stehle T, Truhn D, Aach T, Trautwein C, Tischendorf J. Institute of Electrical and Electronics Engineers. IEEE Engineering in Medicine and Biology Society. IEEE Signal Processing Society. Camera calibration for fish-eye lenses in endoscopy with an application to 3D reconstruction. From Nano to Macro. 2007;4th IEEE International Symposium on Biomedical Imaging; 2007 April 12-15; Arlington, VI, USA. Piscataway: IEEE; p. 1176–1179.
  • 13. Kong SH, Oh BM, Yoon H, et al. Comparison of two- and three-dimensional camera systems in laparoscopic performance: a novel 3D system with one camera. Surg Endosc 2010;24:1132–1143.ArticlePubMed
  • 14. Nakatani H, Abe K, Miyakawa A, Terakawa S. Three-dimensional measurement endoscope system with virtual rulers. J Biomed Opt 2007;12:051803.Article
  • 15. Hasegawa K, Sato Y. Endoscope system for high-speed 3D measurement. Syst Comput Jpn 2001;32:30–39.Article
  • 16. Yamaguchi M, Okazaki Y, Yanai H, Takemoto T. Three-dimensional determination of gastric ulcer size with laser endoscopy. Endoscopy 1988;20:263–266.ArticlePubMed
Fig. 1
An example of distorted image by an endoscope. Fish-eye lens utilized in endoscope causes barrel distortion of the original image (A), rendering distorted images (B, C, D).
ce-45-182-g001.jpg
Fig. 2
Correction of barrel distortion and perspective distortion. To be able to use images obtained by endoscopes for further analysis, the original image should be preprocessed by correcting the barrel distortion and perspective distortion.
ce-45-182-g002.jpg
Fig. 3
An example of stereo-images. Stereo-image is a pair of images captured by two cameras. Matching is the process of finding the corresponding position of the point on the left image with that of the right image. Disparity is relative position of a point in an image.
ce-45-182-g003.jpg
Fig. 4
Epipolar geometry. When the points connecting M, M1, M2, etc. are observed from CL, it is observed as a dot on its image plane as mL, but when these points are observed from CR, it is observed as a line on its image plane as eR-mR.
ce-45-182-g004.jpg
Fig. 5
Two view geometry of cameras. In this model, d12 is the distance between two cameras, f the focal length, L the distance between the cameras and the object, and v1-v2 the disparity.
ce-45-182-g005.jpg
Fig. 6
Pinhole camera model. In this model, f is the focal length, C the camera centre, c the image centre, h the image point of H, and L the distance between the camera center and the object.
ce-45-182-g006.jpg
Fig. 7
The stereo-image of Borrmann type I tumor model. The matching point was (left, 374, 241) and (right, 265, 231), and the resulting disparity was 106 pixels.
ce-45-182-g007.jpg
Fig. 8
The stereo-image of preliminary Borrmann type I tumor experimental model. When two endoscopes of the same model and equal illuminating power were used simultaneously to obtain stereo-images, light interference occurred, leaving behind artifacts resembling a comet's tails.
ce-45-182-g008.jpg
Table 1
Results of the Calculated Distance (L) and the Measurement Error between the Endoscope and the Borrmann Type I Tumor Model
ce-45-182-i001.jpg

f, focal length; d12, distance between two camera; v2-v1, disparity; L, distance between the cameras and the object.

Table 2
Results of the Calculated Height and Width, and the Measurement Error of the Borrmann Type I Tumor Model
ce-45-182-i002.jpg

h, image point of H; H, calculated image size (height and weight).

Figure & Data

REFERENCES

    Citations

    Citations to this article as recorded by  
    • Three-dimensional light-field microendoscopy with a GRIN lens array
      Tara M. Urner, Andrew Inman, Benjamin Lapid, Shu Jia
      Biomedical Optics Express.2022; 13(2): 590.     CrossRef
    • 3D light-field endoscopic imaging using a GRIN lens array
      Changliang Guo, Tara Urner, Shu Jia
      Applied Physics Letters.2020;[Epub]     CrossRef
    • Current and emerging robotic assisted intervention for Notes
      Siyang Zuo, Shuxin Wang
      Expert Review of Medical Devices.2016; 13(12): 1095.     CrossRef
    • Application of robotics in gastrointestinal endoscopy: A review
      Baldwin Po Man Yeung
      World Journal of Gastroenterology.2016; 22(5): 1811.     CrossRef
    • Quantitative analysis of velopharyngeal movement using a stereoendoscope: accuracy and reliability of range images
      Asuka Nakano, Katsuaki Mishima, Ruriko Shiraishi, Yoshiya Ueyama
      Computer Aided Surgery.2015; 20(1): 29.     CrossRef
    • The Evolution of the Conventional Endoscope in an Era of 3-Dimensional Technology
      Geun Am Song
      Clinical Endoscopy.2012; 45(3): 181.     CrossRef

    • PubReader PubReader
    • ePub LinkePub Link
    • Cite
      CITE
      export Copy Download
      Close
      Download Citation
      Download a citation file in RIS format that can be imported by all major citation management software, including EndNote, ProCite, RefWorks, and Reference Manager.
      Format:
      • RIS — For EndNote, ProCite, RefWorks, and most other reference management software
      • BibTeX — For JabRef, BibDesk, and other BibTeX-specific software
      Include:
      • Citation for the content below
      Feasibility of Obtaining Quantitative 3-Dimensional Information Using Conventional Endoscope: A Pilot Study
      Clin Endosc. 2012;45(3):182-188.   Published online August 22, 2012
      DOI: https://doi.org/10.5946/ce.2012.45.3.182
      Close
    • XML DownloadXML Download
    Figure
    • 0
    • 1
    • 2
    • 3
    • 4
    • 5
    • 6
    • 7
    Feasibility of Obtaining Quantitative 3-Dimensional Information Using Conventional Endoscope: A Pilot Study
    Image Image Image Image Image Image Image Image
    Fig. 1 An example of distorted image by an endoscope. Fish-eye lens utilized in endoscope causes barrel distortion of the original image (A), rendering distorted images (B, C, D).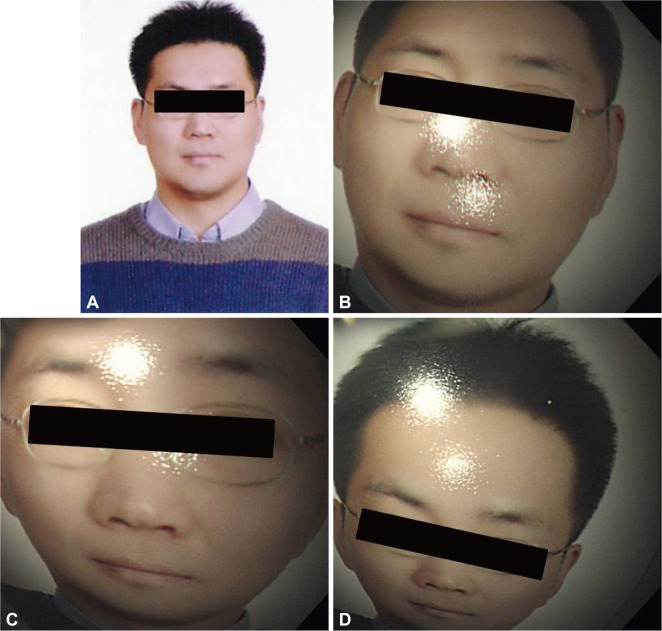
    Fig. 2 Correction of barrel distortion and perspective distortion. To be able to use images obtained by endoscopes for further analysis, the original image should be preprocessed by correcting the barrel distortion and perspective distortion.
    Fig. 3 An example of stereo-images. Stereo-image is a pair of images captured by two cameras. Matching is the process of finding the corresponding position of the point on the left image with that of the right image. Disparity is relative position of a point in an image.
    Fig. 4 Epipolar geometry. When the points connecting M, M1, M2, etc. are observed from CL, it is observed as a dot on its image plane as mL, but when these points are observed from CR, it is observed as a line on its image plane as eR-mR.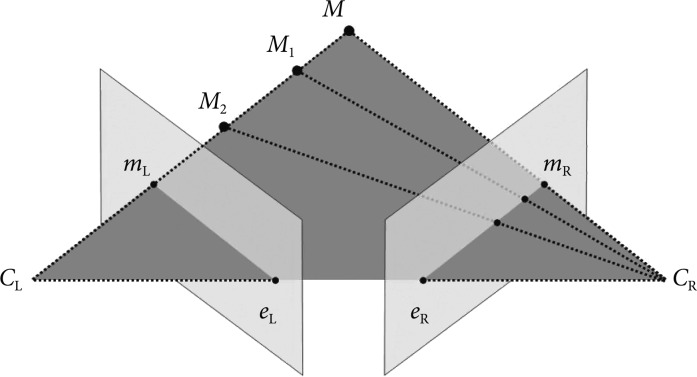
    Fig. 5 Two view geometry of cameras. In this model, d12 is the distance between two cameras, f the focal length, L the distance between the cameras and the object, and v1-v2 the disparity.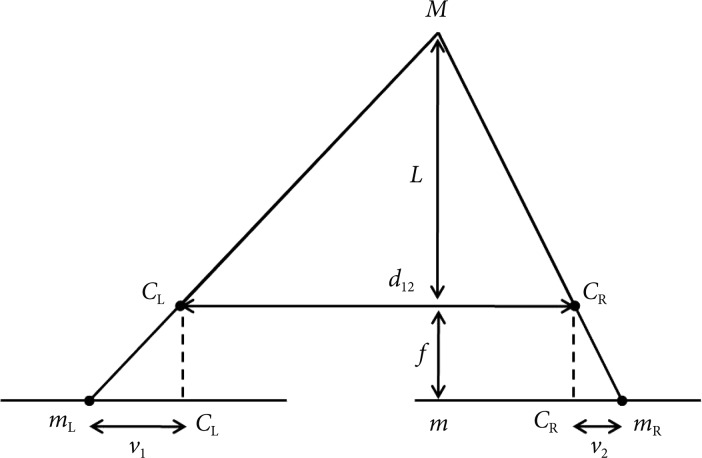
    Fig. 6 Pinhole camera model. In this model, f is the focal length, C the camera centre, c the image centre, h the image point of H, and L the distance between the camera center and the object.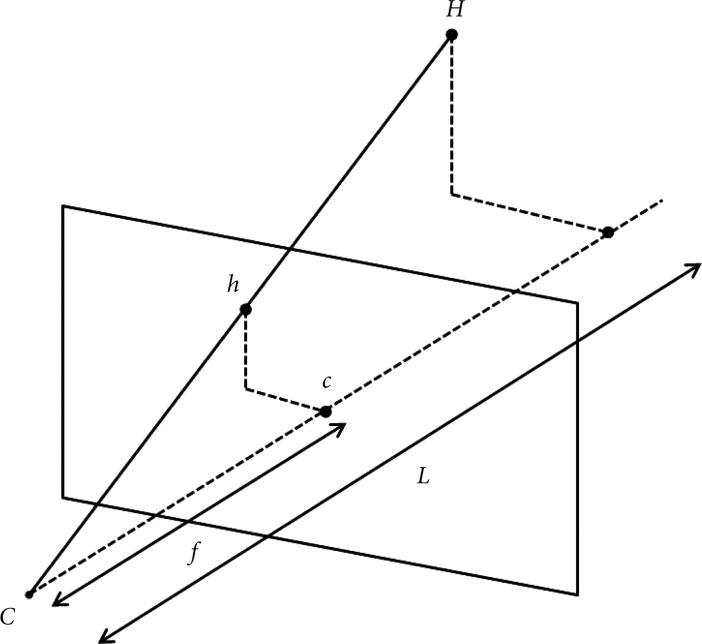
    Fig. 7 The stereo-image of Borrmann type I tumor model. The matching point was (left, 374, 241) and (right, 265, 231), and the resulting disparity was 106 pixels.
    Fig. 8 The stereo-image of preliminary Borrmann type I tumor experimental model. When two endoscopes of the same model and equal illuminating power were used simultaneously to obtain stereo-images, light interference occurred, leaving behind artifacts resembling a comet's tails.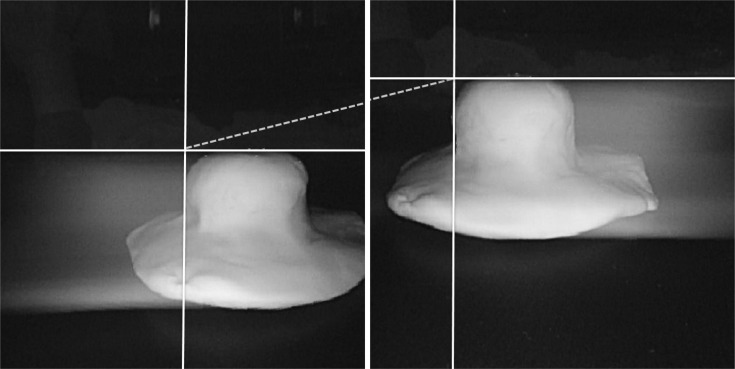

    Fig. 1

    Fig. 2

    Fig. 3

    Fig. 4

    Fig. 5

    Fig. 6

    Fig. 7

    Fig. 8

    Feasibility of Obtaining Quantitative 3-Dimensional Information Using Conventional Endoscope: A Pilot Study

    Results of the Calculated Distance (L) and the Measurement Error between the Endoscope and the Borrmann Type I Tumor Model

    f, focal length; d12, distance between two camera; v2-v1, disparity; L, distance between the cameras and the object.

    Results of the Calculated Height and Width, and the Measurement Error of the Borrmann Type I Tumor Model

    h, image point of H; H, calculated image size (height and weight).
    Table 1 Results of the Calculated Distance (L) and the Measurement Error between the Endoscope and the Borrmann Type I Tumor Model

    f, focal length; d12, distance between two camera; v2-v1, disparity; L, distance between the cameras and the object.

    Table 2 Results of the Calculated Height and Width, and the Measurement Error of the Borrmann Type I Tumor Model

    h, image point of H; H, calculated image size (height and weight).

    Table 1

    Table 2

    Clin Endosc : Clinical Endoscopy Twitter Facebook
    © Korean Society of Gastrointestinal Endoscopy.
    Close layer
    TOP